高二数学寒假作业(二)：立体几何(B)

　　高二数学寒假作业(二)

　　立体几何(B)

　　一、填空题（本大题共10小题，每小题5分，共50分）

　　1.下列命题： ①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行。 其中为真命题的是___________

　　2.长方体的表面积为22cm2，所有棱长和为24cm，则对角线长是___________

　　3.若正四棱柱ABCD-A1B1C1D1的底面边长为1，AB1与底面ABCD成60°角，则A1C1到底面ABCD的距离为__________

　　4.用半径为r的半圆铁皮卷成一个圆锥，则圆锥的高等于__________

　　6.在三棱柱ABC-A1B1C1中，各棱长相等，侧掕垂直于底面，点D是侧面BB1C1C的中心，则AD与平面BB1C1C所成角的大小是___

　　7.已知α，β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β”是“m⊥β”的_________

　　8.给定下列四个命题：①垂直于同一个平面的两个平面平行；②垂直于同一个直线的两个平面平行；③垂直于同一个平面的两条直线平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。其中，为真命题的序号是________

　　9.已知三个球的半径R1，R2，R3满足R1+2R2=3R3，则它们的表面积S1，S2，S3，满足的等量关系是__________

　　10.在正方体ABCD-A1B1C1D1中，二面角C-BD-C1的正切值等于_________

　　二、解答题（共4题，11题10分，12题12分13、14题14分，共50分）

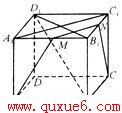
　　11.如图所示正方体ABCD—A1B1C1D1中，M、N分别是A1B1、B1C1的中点。问：

　　(1)AM和CN是否是异面直线？说明理由。

　　(2)D1B和CC1是否是异面直线？说明理由。

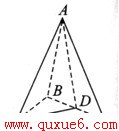
　　12.如图，过S引三条长度相等但不共面的线段SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平面ABC⊥平面BSC。

　　13.如图，在四面体ABCD中，CB=CD,AD⊥BD，点E，F分别是AB，BD的中点求证：(1)直线EF∥面ACD；(2)平面EFC⊥面BCD。

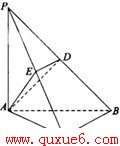
　　14.如图，三棱锥P-ABC，PA⊥面ABC,PA=AB,∠ABC=60°，∠BCA=90°，点D,E分别在棱PB,PC上，且DE∥BC。

　　(1)求证：BC⊥面PAC。

　　(2)求证：DE⊥面PAC。

　　(3)当D为PB的中点时，求AD与平面PAC所成的角的大小。

　　寒假快到了，高二的同学们在放寒假的时候可别忘了自己的学习噢!以上内容是www.quxue6.com小编整理的高二数学寒假作业，希望大家好好利用！