集合概念、知识点及练习题

　　模糊集合这一概念的出现使得数学的思维和方法可以用于处理模糊性现象，从而构成了模糊集合论(中国通常称为模糊性数学)的基础。

　　幂集

　　定义：设有集合A，由集合A所有子集组成的集合，称为集合A的幂集。

　　定理：有限集A的幂集的基数等于2的有限集A的基数次方。

　　并、交集

　　并集定义：由所有属于集合A或属于集合B的元素所组成的集合，记作A∪B(或B∪A)，读作“A并B”(或“B并A”)，即A∪B={x|x∈A,或x∈B}。并集越并越多。

　　交集定义：由属于A且属于B的相同元素组成的集合，记作A∩B(或B∩A)，读作“A交B”(或“B交A”)，即A∩B={x|x∈A,且x∈B}。交集越交越少。

　　若A包含于B，则A∩B=A，A∪B=B

　　补集

　　相对补集定义：由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作A-B，即A-B={x|x∈A，x∉B'}

　　绝对补集定义：A关于全集合U的相对补集称作A的绝对补集，记作A'或?u(A)或~A。·U'=Φ;Φ‘=U

十、运算

　　交换律：A∩B=B∩A A∪B=B∪A

　　结合律：A∪(B∪C)=(A∪B)∪C A∩(B∩C)=(A∩B)∩C

　　分配对偶律：A∩(B∪C)=(A∩B)∪(A∩C) A∪(B∩C)=(A∪B)∩(A∪C)

　　对偶律：(A∪B)^C=A^C∩B^C (A∩B)^C=A^C∪B^C

　　同一律：A∪Φ=A A∩U=A

　　求补律：A∪A'=U A∩A'=Φ

　　对合律：(A')'=A

　　等幂律：A∪A=A A∩A=A

　　零一律：A∪U=U A∩U=A

　　吸收律：A∪(A∩B)=A A∩(A∪B)=A

　　德·摩根定律(反演律)：(A∪B)'=A'∩B' (A∩B)'=A'∪B'

　　德摩根律：1.集合A与集合B的交集的补集等于集合A的补集与集合B的补集的并集; 2.集合A与集合B的并集的补集等于集合A的补集与集合B的补集的交集。 容斥原理(特殊情况)：card(A∪B)=card(A)+card(B)-card(A∩B)

　　card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(C∩A)+card(A∩B∩C)

　　容斥原理基本思想：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

　　【练习题】

　　1、下列四组对象，能构成集合的是( )

　　A.某班所有高个子的学生　B.著名的艺术家　C.一切很大的书　D.倒数等于它自身的实数

　　2、集合{a，b，c }的真子集共有( )个

　　A.7 　　B.8 　　C.9 　　D.10

　　3、点的集合M={(x,y)|xy≥0｝是指( )

　　A.第一象限内的点集　　　　　B.第三象限内的点集

　　C.第一、第三象限内的点集　　D.不在第二、第四象限内的点集

　　4、

　　5、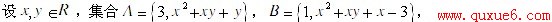y的值

　　【参考答案】

　　1、D

　　2、A

　　3、D

　　4、

　　5、

上一页  [1] [2] [3] [4] [5] [6]