12-26 23:26:40 浏览次数:136次 栏目:小学四年级数学教案
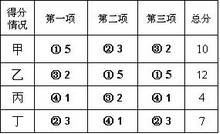
推理过程:
假设甲在第一项比赛中获得第一名5分,在第二项比赛中获得第二名3分,在第三项比赛中获得第三名2分。
则乙得了2个第一名,就是第二项和第三项的第一名得5分,乙只能在第一项得了第三名2分。
丙得了一个第三名,两个第四名。第一项和第三项的第三名已经有主,丙只能得第二项的第三名2分,剩下丙在第一项、第三项就是得了第四名1分。
丁得了两个第二名,一个第四名,是第二项的第四名1分,第一、三项的第二名,分别得3分。
《奥赛天天练》第49讲,巩固训练,习题1
【题目】:
甲、乙、丙、丁比赛乒乓球,每两个人要赛一场,结果甲胜了丁,并且甲、乙、丙三人胜的场数相同,问丁胜了几场?
【解析】:
假设、推理、反证:
四人比赛,每两个人要赛一场,共有6场比赛:3+2+1=6,每场比赛一胜一负,共有6胜、6负。
因为甲、乙、丙三人胜的场数相同,已知的甲已经胜了一场,所以这三人平均每人最少可能胜了1场,最多可能胜了2场。
假设甲、乙、丙三人平均每人胜了1场,共胜3场,则丁一个人胜了3场,即丁同时胜了甲、乙、丙三人,与已知条件“甲胜了丁”矛盾,即这个假设是错误的。
所以,真实的结果是甲、乙、丙三人平均每人胜了2场,即丁胜了0场。
倒推验证:
根据上面结论,甲、乙、丙三人都胜了丁,各得1场胜。
然后,这三人相互之间,只要循环战胜(例如甲胜了乙;乙胜了丙;丙胜了甲),即每人再一胜一负。
可得:甲、乙、丙三人平均每人胜2场,丁胜0场成立。
tag: 逻辑推理 小学四年级数学教案,四年级下册数学教案,小学数学教案,免费教案 - 数学教案 - 小学四年级数学教案